Vorig schooljaar gaf ik enkele maanden wiskundeles aan leerlingen uit de derde graad ASO1. Aangezien ik zo’n vijftien jaar geleden op dezelfde school gezeten heb, was het boeiend om te zien wat er in die tijd veranderd is.
Inhoud, didactiek en technologie
Wat meteen opviel, was dat de onderwerpen bijna niet veranderd zijn. De leerlingen krijgen nog steeds analyse, ruimtemeetkunde, statistiek en kansrekenen, complexe getallen en matrices en stelsels.
Ook de manier van lesgeven is in essentie gelijk gebleven. De leraar werkt de leerstof uit aan het bord2. In de leerboeken worden stukjes theorie gevolgd door verwerkingsoefeningen.
Er zijn wel enkele hulpmiddelen bijgekomen. De wiskundeleraar moet geen ingewikkelde (ruimte)figuren meer tekenen op het bord. Je kan immers de figuur uit de digitale versie van het handboek projecteren. Voor analyse zijn de computer en projector nog handiger. Met software zoals Geogebra kan je direct tonen hoe de grafiek van een functie er uit ziet. Bij functies met een parameter kan je de parameter variëren en het gevolg onmiddellijk zien in de grafiek.
Het is niet enkel de leraar die extra ‘speelgoed’ ter beschikking heeft. Met hun grafische rekenmachine kunnen de leerlingen zelf ook grafieken plotten. Terwijl vorige generaties bijvoorbeeld matrices met de hand moesten inverteren en waarschijnlijkheden opzoeken in tabellen, kunnen scholieren dat nu allemaal met de rekenmachine.
Nochtans worden de technologische mogelijkheden zeker niet ten volle benut. Bij zijn afscheid van de TU Delft in 2003 schreef de onlangs overleden Nederlandse wiskundeprofessor Jan Aarts in het artikel ‘Was ik nu maar wiskundeleraar’3:
Een groot deel van de rekenkunde is slavenarbeid. En waar het mogelijk is, moeten we dat door een machine laten doen.
Onder de slavenarbeid van de wiskunde verstond professor Aarts “differentiëren, primitiveren, het berekenen van bepaalde integralen, het oplossen van differentiaalvergelijkingen, kortom bijna alles wat nu in de wiskundelessen wordt onderwezen.”
Hoewel er gratis software bestaat die afgeleiden en integralen kan berekenen, moeten de leerlingen deze slavenarbeid vijftien jaar later nog steeds met de hand doen.
Verloren vaardigheden?
Het gebruik van de rekenmachine heeft ook een keerzijde. Naarmate leerlingen de rekenregels en -methodes minder expliciet met de hand toepassen, worden ze minder automatismen.
Neem bijvoorbeeld het volgend probleem,
27 x2 + 45 x – 18 = 0 (1)
Dit is een vierkantsvergelijking (VKV). Vierkantsvergelijkingen zijn leerstof uit het vierde jaar die ook regelmatig in de derde graad opduiken.
De leerlingen weten dat ze de wortels van (1) kunnen vinden via de formule
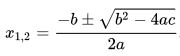
waarbij a = 27, b = 45 en c = -18.
Maar zelfs met de rekenmachine is het gemakkelijk om fouten te maken bij de invoer of het overschrijven van de stappen in de berekening.
Je kan echter ook de VKV handmatig oplossen door op te merken dat de coëfficiënten a, b en c veelvouden zijn van 9. Zo kan je het probleem vereenvoudigen.
Beide leden van (1) delen door 9 geeft
3 x2 + 5 x – 2 = 0 (2)
Invullen van gehele getallen met een kleine absolute waarde toont aan dat x = -2 voldoet aan de VKV, zodat we (2) kunnen herschrijven als
(x + 2)(3x – 1) = 0
De wortels zijn dus x1 = -2 en x2 = 1/3. Geen rekenmachine nodig!4 Maar zelfs wie toch de rekenmachine wil gebruiken, loopt bij de vereenvoudigde vorm (2) minder kans op fouten.
Het gebrek aan routine is ook merkbaar bij het inverteren van matrices. Wanneer alle elementen van de matrix getallen zijn, kan je met de rekenmachine de oplossing vinden. Matrices met symbolen kan de rekenmachine (voorlopig) nog niet aan. In zo’n geval is het handig dat je de Gauss-Jordaneliminatie onder de knie hebt.
Het is ook lastig om bewijzen en wiskundige afleidingen te volgen als je bij elke stap moet nadenken over de gebruikte rekenregel.
Nauwkeurig kunnen rekenen – eventueel deels met de rekenmachine – is een niet te onderschatten vaardigheid. In dit opzicht verschil ik van mening met professor Aarts (zie verder).
De toekomst
Professor Aarts was dan misschien te optimistisch over de timing, in grote lijnen had hij zeker gelijk. Computers nemen de slavenarbeid van de leerlingen over. Daardoor zal er meer tijd zijn voor andere zaken. Aarts schreef daarover in 2003:
De wiskunde die wij onderwijzen dient een afspiegeling te zijn van de levende wiskunde. Begrippen en ideeën zijn meestal niet spontaan, in een flits ontstaan, maar zijn bijna altijd gevormd in een langdurig en moeizaam proces; het is mensenwerk.
Bij de behandeling van een begrip kan men niet voorbijgaan aan de plaats van dat begrip binnen de wiskunde en de andere wetenschappen. Er moet aandacht zijn voor de achterwaartse, voorwaartse en zijwaartse relaties, anders gezegd, aan het waarom, het waarheen en het waartoe.
en verder:
De pc opent [door het elimineren van manueel rekenwerk] onverwachte mogelijkheden om het wiskundeonderwijs opnieuw in te richten. De leerlingen hoeven niet eerst de regels te leren, maar kunnen zich meteen richten op het verkrijgen van meer inzicht in de leerstof. Er komt ruimte om weer aandacht te besteden aan het waarom, het waarheen en het waartoe.
In plaats van uren te spenderen aan integratietechnieken, kan er in de toekomst meer tijd gaan naar het vertalen van vraagstukken in vergelijkingen, die de computer vervolgens uitrekent. De klas kan de oplossingen die uit de computer komen ook grondiger bespreken dan nu meestal het geval is. “Houdt deze oplossing steek? Hoe kunnen we dit resultaat controleren? Welke aannames zijn belangrijk en wat gebeurt er als we die veranderen?”
De leraar kan ook vragen om een probleem op verschillende manieren op te lossen. Zo worden de verbanden tussen de deelgebieden van de wiskunde in de verf gezet.
Welke onderwerpen zullen zestien- en zeventienjarigen in de ‘zware’ wiskunderichtingen binnen twintig jaar voorgeschoteld krijgen? Analyse en lineaire algebra zullen ongetwijfeld deel blijven uitmaken van het programma. Wie (toegepaste) wetenschappen of economie volgt in het hoger onderwijs heeft die wiskunde immers nodig.
Misschien zal door het belang van de computer ook numerieke wiskunde aan het lessenpakket van het middelbaar toegevoegd worden. Zo komen de leerlingen in contact met de algoritmes die de slavenarbeid voor hen uitvoeren.
Verder voorspel ik dat er nog meer dan vandaag aandacht zal zijn voor statistiek, maar dat is voer voor een andere post.
Een ingekorte versie van deze post verscheen ook op de website van EOS Wetenschap.
- Ter info: mijn leerlingen volgden zes of acht uur wiskunde per week.
- Nu een bord met stiften, toen een krijtbord.
- ‘Was ik nu maar wiskundeleraar’, Natuurwetenschap & Techniek, september 2003, p.60-62
- Alternatief kan je de som- en productformules gebruiken om de oplossingen van de VKV te vinden.
